Graph Theory
What is a Graph
Introduction
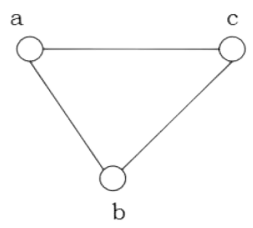
Let \(G = (V, E)\), where \(V\) is a set of vertices and \(E \subseteq\) \(\) \(\left\{\left\{x, y\right\}\;|\;x, y \in V\;and\;x \neq y\right\}\). A simple undirected graph \(G\) is an ordered pair or tuple \((V, E)\) where \(V\) and \(E\) are finite sets.
\(E \subseteq\) \( \left\{\left\{x, y\right\}\;|\;x, y \in V\;and\;x \neq y\right\}\) states that the elements that are apart of set of edges \(E\) are unordered pairs. Where the elements that make up our ordered pair for our edge are elements from our set \(V\). Meaning, in order to define an edge from \(E\), its elements or vertices must came frome set the \(V\). Our two elements of our edge are our head and tail vertice. These two vertices define an edge or the elements of \(E\).
It is important to note that in our defintion that defines our edges in our simple graph, the edges that make up our set \(E\) are unordered pairs or tuples. This means that it does not matter which vertice is the head or tail vertice. i.e. which vertice comes first and which vertice comes last. Meaning we do not have a start and end vertice for our edges, and do not care about the direction of our vertice. Rather, all that matters is we define the vertices that make up our edges and that they are apart of the vertices in our graph \(V\). Unlike in a directed graph where an ordered pair defines each edge and direction of the edge matters.
The reason I introduced the simple undirected graph is because it allows us to get familiar with the mathematical notation that we will build upon for other graphs and is one of the most common type of graphs.
Graph Types
We will now talk about a couple of different graphs that exist, more specifically ones that are commonly used.
Simple Directed Graph
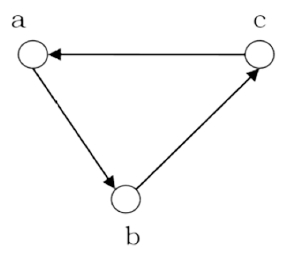
Let \(G = (V, E)\) where \(V\) is a set of vertices and \(E \subseteq\) \( \left\{(x, y)\;|\;(x, y) \in V^{2}\;and\;x \neq y\right\}\). Notice in this one the difference is that the elements in set \(E\), or the set of Edges, are tuples or ordered pairs not unordered pairs like with a directed graph. Why do the edges in the Edges set, \(E\) need to be defined as an ordered pair? Well, because since the elements in our ordered pair are vertices in the graph, this means mathematically, \((x, y) \neq (y, x)\). i.e, the order matters. Thus, in the ordered pair of elements or vertices, which vertice or element in the tuple is the head and which one is the tail matters. In an unordered pair, or a set, it does not matter which one is first or last, it is more so which vertices make up the edge. So, for an edge in in the set of edges \(E\) in a directedd graph, we define the collection as an ordered pair or by using a tuple.
For the vertices that make up our ordered pair of edges, it does not suffice to give the rule that the vertices \(x, y \in V\) or that our vertices are elements in \(V\). This rule and the procedding rule in the set builder notation for \(E\) in a directed graph does not produce an ordered pair. Rather, we must change it to \((x, y) \in V^{2}\). Reason being is because \(V^{2}\) is equivalant as writing \(V \times V\), or the cartesian product between set \(V\) and set \(V\). The cartesian product between sets forms one set whose elements are ordered pairs of the original sets. The general name for raising a set to \(n\), is called an \(n\)-ary cartesian product. For example, if we had some set \(X\), the \(n\)-ary cartesian product of set \(X\) would be written as \(X^{n}\). Another thing to note, is that raising a set to \(2\), like in our case, it is called the cartesian square.
So now, with that being said, with our updated rule we can take an element from our set \(V^{2}\) are get an ordered pair, like is necessary for a directed graph. When before, with an element coming from just \(V\), we were simply taking one element from the set of vertices.
Loop Permitting Graphs
Consider an undirected simple graph permitting loops. Let \(G = (V, E)\) \(V\) is a set of vertices and \(E \subseteq\) \( \left\{\left\{x, y\right\}\;|\;x, y \in V\right\}\) Notice how our set of edges \(E\) is defined similarily to the Edge set of our previous non-loop permitting directed simple graph \(E \subseteq\) \( \left\{(x, y)\;|\;(x, y) \in V^{2}\;and\;x \neq y\right\}\), however, in the definition for \(E\) in our loop permitting graph the vertices, \(x\) and \(y\), for each edge can be the same vertice. This is because in our rule for loop permitting graphs in our definition for \(E\) it does not have the rule \(x \neq y\). i.e, our updated definition for for our directed graph that allows for edges to have the same start and end vertice, or allows for the head and tail vertice to be the same vertice.
Multigraphs
Consider a directed multigraph. Let \(G = (V, E, \phi)\) where \(V\) is a set of vertices, \(E\) is a set of edges, and \(\phi : E \) \(\rightarrow \left\{(x, y)\;|\;(x, y) \in V^{2}\; and \;x \neq y\right\}\)
Weighted Graph
To continue.