Topological Quantum Field Theory

Introduction

Topological quantum field theory TQFT in physics uses the zero-energy sector of the Hilbert space of states that does not include time, which the Hamiltonian eliminates. Mathematically, TQFT is used as an organizing structure for topological or differential invariant manifolds. A \(D\)-dimensional TQFT as a symmetric monoidal factor is given as:

\(Z:\left(\mathscr{B}ord_D^{o r}, \amalg\right) \rightarrow(V ect, \otimes)\)

\(\mathscr{B}ord_D^{o r}\) is a category of compact objects, boundary-less oriented \((D-1)\)-dimensional manifolds, where morphisms are oriented \(n\)-dimensional bordisms, modulo diffeomorphism relative to the boundary. The bordism has an incoming and outgoing boundary, however, in an oriented world the boundary orientation can be compared on each component with independent orientation.

The bordism category has a symmetric monoidal structure defined by the disjoint union. This structure has an associative and commutative multiplication functor:

\(\amalg: \mathscr{B}ord_D^{o r} \times \mathscr{B}ord_D^{o r} \rightarrow \mathscr{B}ord_D^{o r}\)

Note, that multiplication for the category of vector spaces is similar, however, it is instead defined by the tensor product and is called the tensor structure. This structure includes additional linearity properties of \(V ect\) and the bi-linearity of \(\otimes\).

To continue, we will look first at finite group gauge theory as it realtes to TQFT, two-dimensional guage theory, extended TQFT, cobordism hypothesis in dimensions 1 and 2, and then look at cobordism hypothesis in a higher dimension. Let's begin!

Finite Group Gauge Theory

First let us look at an example of finite group guage theory \(Z_F\) that does not use orientations and is associated with a finite group \(F\). This theory can be constructed relatively eaiser than others in higher dimensions, however, it can only detect fundamental groups of manifolds. First, consider the groupoid of principal \(F\)-bundles over some manifold \(X\), which we will denote as \(\text {B}un_F (X)\). Next, given a closed \(D\)-dimensional Manifold \(M\), \(Z_F\) will assign the number of isomorphism classes that is a part of principal \(F\)-bundles on \(M\) where each is weighted down by its automorphism group. Looking back at the manfiold \(M\), the assigned number is equal to \(\# H o m\left(\pi_1(M), F\right) / \# F\). This means that in one dimension, \(Z_F\left(S^1\right)=1\). Note, the space of functions on \(Bun_{F}(N)\), given a closed \((D-1)\)-dimensional manifold, is \(Z_F(N)\).

We can see now that \(Z_F(M): Z_F\left(\partial^{-} M\right) \rightarrow Z_F\left(\partial^{+} M\right)\) is a linear map. This map has matrix entry relating \(F\)-bundles \(F^{-} \rightarrow \partial^{-} M\) and \(F^{+} \rightarrow \partial^{-} M\), such that it counts the \(F\)-bundles on manifold \(M\). Here, the count is restricted to specified bundles on the two boundaries and is weighted by automorphisms that are trivial on the outgoing boundry of \(\partial^{+}M\). Note, in order to check that the mapping gives a TQFT, the composition of bordisms need to map to the composition of linear maps.

Two-Dimensional Gauge Theory

Two-dimensional gauge theory gives a TQFT computation for all integrals over the moduli space \(\Phi(\Sigma;G)\), such that there are flat \(G\)-connections on some surface \(\Sigma\) and where the results are given in terms of an explicitly computed Frobenius algebra. Assuming that a \(G\) is simple and simply connected, the dimension for \(\Phi(\Sigma;G)\) is \(2 d=2 \operatorname{dim} G \cdot(g-1)\).

The map \(u\) maps the universal flat bundle over \(\Sigma \times \Phi(\Sigma ; G)\) to the classifying space \(BG\), where \(G\) is a topological group. Every bundle with the given structure \(B\). In terms of homotopy theory, a part of mathematics, we are saying bundle that has the structure group \(G\) the quotient of the weakly contractible space \(BG\), such that every bundle with the given structure group \(G\) over paracompact manifold \(M\) is a pullback by means of a continuous map \(M \rightarrow BG\).

To continue.

Seiberg-Witten Theory

The formula in the case of \(SU(2)\) is as follows. Choose a polynomial \(Q\). For each \(k \in \mathbb{Z}_{+}\), let \(\xi(k, t)\) be the formal power series in \(t\) that represents a unique critical point of the function in \(\xi\):

\(F(\xi ; h, k, t)\) \(:=\frac{1}{2}(\xi-k)^2+t \cdot \frac{h}{2 \pi^2} \cdot Q(\pi \xi / h)\)

where, \(t\) is treated as a formal variable. \(\xi(k,t)\) undergoes \(t\)-series expansion near the minimum \(\xi(k,0)=k\), formulated as:

\(\displaystyle{ \int_{F(\Sigma ; G)} \exp \left\{h \omega+t \cdot[\Sigma] \backslash Q\left(u^* \phi_2\right)\right\} }\) \(\displaystyle{ =\# Z(G) \cdot h^{3 g-3} \operatorname{vol}(G)^{2 g-2} }\) \(\displaystyle{ \sum_{k>0}\left[\frac{1+\frac{t}{2 h} Q^{\prime \prime}(\xi(k, t))}{\xi(t, k)^2}\right]^{g-1} }\)

such that, \(\#Z(G)=2\) for \(SU(2)\).

To continue.

Glossary

Homotopy Theory

To continue.

Polar stereographic projections
Differential Manifolds

An \(n\)-dimensional manifold is a topological space where each point has a neighborhood that is homeomorphic to an open subset on \(n\)-dimensional Euclidean space. Let \(M\) be a topological space. A chart in \(M\) consists of an open subset \(U \subset M\) and a homomorphism \(h\) of \(U\) onto an open subset of \(R^{m}\). A...

Read More
World Line
Compatification and Massless Scattering in Anti-de Sitter Space

In theoretical physics, Minkowski Space is a particular type of \(4\)-dimensional Lorentzian space, with a Minkowski metric. Where the Minkowski metric is a metric tensor denoted as \(d\tau^2\) with the form \(-\left(d^0\right)^2+\left(d x^1\right)^2\) \(+\;\left(d x^2\right)^2+\left(d x^3\right)^2\). Minkowski space forms the basis of the study of spacetime within special relativity and is...

Read More
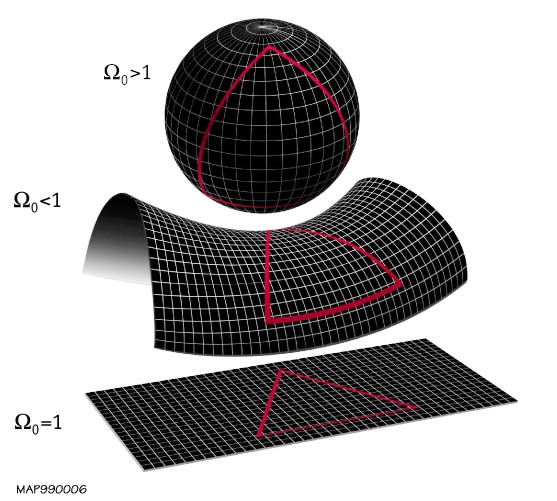
End of universe
Quantum Fields in Anti-de Sitter Space and the Maldacena Conjecture

In theoretical physics, the Maldacena Conjecture states supergravity and string theory on the product of \((n+1)\)-dimensional Anti-de Sitter space with a compact manifold capable of describing large \(N\) limits of conformal field theories in \(d\)-dimensions. Correlation functions in CFT are dependent on the supergravity action of asymptotic behavior at infinity...

Read More