Differential Manifolds
Differential Structures
Manifolds
An \(n\)-dimensional manifold is a topological space where each point has a neighborhood that is homeomorphic to an open subset on \(n\)-dimensional Euclidean space. Let \(M\) be a topological space. A chart in \(M\) consists of an open subset \(U \subset M\) and a homomorphism \(h\) of \(U\) onto an open subset of \(\mathbb{R}^{m}\). A \(C^{r}\) atlas on \(M\) is a collection \(\left\{U_{\alpha}, h_{\alpha}\right\}\) of charts such that the \(U_{\alpha}\) cover \(M\) and \(h_{\beta}h_{\alpha}^{-1}\), the transition maps, are \(C^{r}\) maps on \(h_{\alpha}(U_{\alpha}\cap U_{\beta})\).
A maximal atlas \(C^{r}\) on \(M\) is called a \(C^{r}\) structure. A differential manifold \(M\) of class \(C^{r}\) has a second countable Hausdorff space \(M\) and is equipped with a \(C^{r}\) structure on it. A \(C^{\infty}\) atlas, being a chart, structure, etc., will be refered to as smooth throughout the rest of this article.
Smooth Mainfold
Given an open subset \(U\subset \mathbb{R}^{n}\), a function \(f:U\rightarrow M\subset\mathbb{R}^{A}\), is smooth if for all functions \(f_{\alpha}:U\rightarrow\mathbb{R}\) is smooth. Where \(R^{A}\) denotes the vector space of all functions \(x\). Given \(f\) is smooth, the partial derivative \(\frac{\partial_{f}}{\partial_{u_{i}}}\) is defined as a smooth function \(U\rightarrow\mathbb{R}^{A}\), where for the \(\alpha\)-th coordinate is \(\frac{\partial_{\alpha}}{\partial_{u_{i}}}\) for \(i=1,...,n\).
A good method of studying smooth manifolds is by putting together the smooth manifold with smaller pieces. These smaller pieces themselves are not smooth manifolds, but rather manifolds with boundary. The definition of a manifold parallels a manifold definition (defined in the Manifolds section) however, we need to update the definition of a homeomorphism. For a manifold with boundary, the homeomorphisms \(h_{\alpha}\) onto the open subsets of \(\mathbb{R}^{m}\) or \(\mathbb{R}^{m}_{+}\), where \(\mathbb{R}^{m}_{+}=\left\{(x_{1},...,x_{m})\in\mathbb{R}^{m}|\;x_{m}\ge 0\right\}\). Meaning, with our update when an open subset of our topological structure is passed through the homeomorphic functions \(h_{\alpha}\), it can now be mapped surjectively to the eucledian space of \(\mathbb{R}^{m}\) or \(\mathbb{R}^{m}_{+}\). Where for \(\mathbb{R}^{m}_{+}\), the last element in the ordered pair of real elements is \(\ge 0\). To put it succently, the transtion maps now become maps of open subsets of \(\mathbb{R}^{m}_{+}\). This type of map is smooth if it is locally a restriction of a smooth map defined on an open subset of \(\mathbb{R}^{m}\), by definition.
Riemannian Manifold
A Riemannian manifold is a smooth manifold \(M\) with a Riemannian metric denoted \((M,g)\). For every point \(p\in M\) the tangent bundle of \(M\) assigns a vector space \(T_{p}M\), termed the tangent space of \(M\) at \(p\). The Riemanniam metric defines a positive-definite inner product:
\(g_p: T_p M \times T_p M \rightarrow \mathbb{R}\)
with a norm \(|\cdot|_p: T_p M \rightarrow \mathbb{R}\) given as:
\(|v|_p=\sqrt{g_p(v, v)}\)
Partitions of Unity
In differential topology, many constructions utilize partitions of unity. Before we continue, we will formally define a specific type of atlas. This is an atlas \(\left\{U_{\alpha},h_{\alpha}\right\}\) on \(M\) that is said to be adequate if it is locally finite, \(h_{\alpha}(U_{\alpha})=\mathbb{R}^{m}\) or \(\mathbb{R}^{m}_{+}\), and \(\bigcup_{\alpha}h^{-1}_{\alpha}(\mathring{D}^{m})=M\).
To continue.
Vector Bundle
A vector bundle is topological construction that has a family of vector spaces parameterized by another space \(X\). This space \(X\) can be a topolgical space, manifold, or another type of algebraic variety. By family, we are refering to more generally a family of sets. This family of sets is a collection \(F\) of subsets over the given set \(S\). More to our case we have a family of sets or vector spaces parameterized over the manifold space \(M\). For vector space, we are refering to a set of vector elements that may be added together and multiplied by numbers or scalars. These scalars often are real numbers but can be complex numbers or another type of element of any field. Speaking more generally, for every point \(x\) of the space \(X\) we we associate a vector space \(V(x)\) such that these vector spaces fit together to form another space of the same kind as \(X\). This resulting same kind of space is called a vector bundle over \(X\).
Trivial Bundle
Trivial vector bundles is where we have a fixed vector space \(V\) such that \(V(x)=V\) for every \(x\) in some space \(X\).
We define this as letting \(E=B\times F\) and let \(\pi: E \rightarrow B\) be defined as the projection onto the first factor. \(\pi\) is a fiber bundle of a family of vector spaces \(F\) over \(B\). Note, here \(E\) is globally a product. Finally, any such fiber bundle is called a trivial bundle.
Smooth Vector Bundle
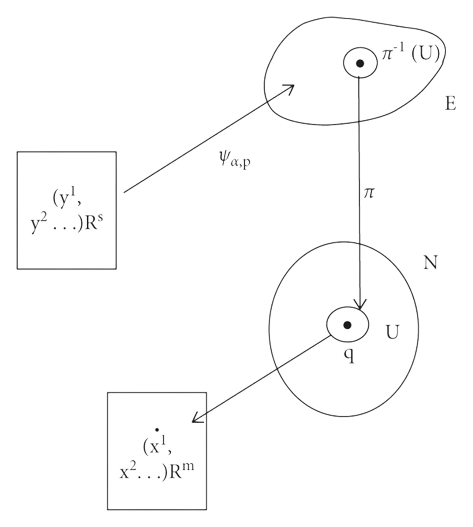
Image Source: Theory and Numerical Simulation of Deep Rock Mass Based on a Non-Euclidean Model
Let \(\pi: E \rightarrow M\) be an \(n\)-dimensional vector bundle over a smooth manifold \(M\). Let \(\left\{U_{\alpha}, h_{\alpha}\right\}\) be an atlas on \(M\) where the vector bundle is trivial over the sets \(U_{\alpha}\). Let \(\phi_{a}\) represent that canonical map defined as \(\pi^{-1}(U_{a})\rightarrow U_{a} \times\mathbb{R}^n\) with a projection onto \(n\)-dimensional Eucledian space \(\mathbb{R}^n\). Here we are taking our open subset \(U_{\alpha}\) of the manifold in topolgical space \(M\) and mapping \(U_{\alpha}\) to \(\mathbb{R}^n\).
With the smooth vector bundle, we take the family of open subsets \(U_{\alpha}\) in atlas \(\left\{U_{\alpha}, h_{\alpha}\right\}\) on toplogical space and pass it through the canonical map to \(n\)-dimensional Eucledian space.
Operations on Manifolds
Connected Sums

This graph represents a connected sum between \(m\)-dimensional manifolds \(M_{1}, M_{2}\). Using the notation:
\(M_{1}\#M_{2}(h_{1}, h_{2}, \alpha)\)
\(=(M_{1}-h_{1}(0))\cup_{g}(M_{2}-h_{2}(0))\)
where \(g=h_{2}\alpha h_{1}^{-1}\)
we can formally define the function for the connected sums between two manifolds.
In our notation \(M_{1}, M_{2}\) are two connected \(m\)-dimensional manifolds. We let \(h_{i}: \mathbb{R}^{m} \rightarrow M_{i}, i = 1,2\), be two imbeddings. \(\alpha\) is an arbritary orientation reversing diffeomorphism whose domain is \((0, \infty)\) and codomain is \((0, \infty)\). Next, we define \(\alpha_{m}: \bf \mathbb{R} - 0 \rightarrow \mathbb{R} - 0\) by:
\(\alpha(v)\;=\;\alpha(|v|) {v \over |v|}\)
The connected sum is then written as \(M_{1}\#M_{2}(h_{1}, h_{2}, \alpha)\).
Handle Presentation Theorem
Cobordism Preliminary
An ordered triple of manifolds \(\mathscr{C}=\left\{V_0, W, V_1\right\}\) where \(\partial W=V_0 \cup V_1\) and \(V_{0}, V_{1}\) are disjoint open subsets of \(\partial W\) is called a cobordism. Such that \(V_0=\partial_{-} W\) is the left-hand boundary of \(W\). \(\{M \times\{0\}, M \times I, M \times\{1\}\}\), where \(M\) is a compact closed manifold, is an example cobordism termed an elementary cobordism of \(\lambda\). The result is attaching a \(\lambda\)-handle to the right-hand boundary of \(M \times I\).
Note, we will view a trivial cobordism as an elementary cobordismof index \(-1\), as it is convient.
Consider two cobordisms \(\mathscr{C}=\left\{V_0, W, V_1\right\}\), \(\mathscr{C}'=\left\{V'_{0}, W', V'_{1}\right\}\), and a diffeomorphism given as \(h:V'_{1}\rightarrow V'_{0}\). Using \(h\), we can join \(W\) and \(W'\), like so: \(W_{1}=W\bigcup_{h}W'\). Let \(\partial W_{1}=V_{0}\cup V'_{1}\) and \(\left\{V_0, W_{1}, V'_1\right\}\) be a cobordism denoted as \(\mathscr{C}\cup \mathscr{C}'\).
Note, that this notation is symbolic and does not show the result dependent on the diffeomorphism \(h\). That being said, given \(\mathscr{C}\) is a trivial cobordism, the result does not depend on \(h\) and therefore the result is given as \(\mathscr{C}\cup \mathscr{C}'\) \(=\) \(\mathscr{C}\).
Handle Presentation Theorem and Morse Theory
The Smale and Wallace theorem is the following. Let \(\mathscr{C}=\left\{V_0, W, V_1\right\}\) be a cobordism, such that \(\mathscr{C}\) \(=\) \(\mathscr{C}_1 \cup \mathscr{C}_2 \;\cup\) \(\cdots\) \(\cup \;\mathscr{C}_k\), where \(\mathscr{C}_i\) are elementary cobordisms. Given \(i < j\) implies \(\lambda(i) \leq \lambda(j)\), where \(\lambda(i)\) denotes the index of \(\mathscr{C}_i\). The corollary is there exists a sequence of manifolds \(V_0 \times I\) \(=\) \(W_{-1} \subset W_0 \subset W_1 \subset\) \(\cdots\) \(\subset W_m=W\) such that \(W_i\) is obtained from \(W_{i-1}\) by attaching \(i\)-handles to the right-hand boundary of the cobordism \(\mathscr{C}\).
To continue.
Glossary
Topological Space
Let us break this down. First, we will start with getting an idea of what a topological space is, since this is one of the first parts of our definition of a manifold. A topological space is roughly speaking where the closeness of the points in the space cannot be numerically defined, unlike in Euclidean space. What is Euclidean space? If you recall, in school we would plot a point in 2-d space using \((x, y)\) and an \(x\) and \(y\) axis with dashes along the side to help define the space between values. This is 2-dimensional Euclidean space. Or written as \(\mathbb{R}^{2}\). Of course, our Euclidean space is not limited to 2 dimensions. We can use similar descriptors for 3-d space, 11-space, and any number of dimensions, or \(n\)-d Euclidean space \(\mathbb{R}^{n}\). However, continuing with 2-d space, using our numbered \(x\) and \(y\) axis and our points with coordinates, we can figure out the numerical value that represents how close one point is to other. However, a topological space, unlike our familiar Eucledian space, is more generalized than that. Rather, our space does not have a "numbered axis" to define one point relation to another. Rather our space is represented as a set of points whose elements are called points. In this set that defines our topological space, we have a structure called a topology. This topology is defined as a set of neighborhoods for every point that, by examining the other points or elements that are in this neighborhood set, gives an idea of closeness or relation of one point to another. So, we have a set of points that defines what makes up our topological space and a structure called a topology that is defined as a set of neighbors.
Topological Structure
A topological structure, roughly speaking, is an additional structure to a topological space that can be defined as a set of neighborhoods. A neighborhood is closely related to an open subset. This is why in our definition, when we take an open subset from our topology we get an open subset. i.e. \(U_{p} \subset T\). Basically, a neighborhood of a point from a topological space is a set of points that contains that point and the points for which we can move around in any direction and still be in our set or neighborhood. This is why our point \(p\) that we have is an element of \(U\). Since when we take a point we want to examine a slice of our topology that contains the point we are examining and not some random point. We do this so we can keep properly traversing through our topology and keep a list of all of the charts and their respective homeomorphisms. This allows us to determine if all elements or open subsets in our topology when sent through their respective homeomorphisms, are a part of eucledian space \(R^{d}\). i.e. if parts of our topological space \(M\) examined locally are apart of eucledian space \(R^{d}\).
Chart
A chart in a topological space \(M\) consists of \(U_{\alpha}\) an open covering that is homeomorphic, via \(h_{\alpha}\) a homeomorphism, to an open subset \(U_{\alpha}\) in Eucledian space \(\mathbb{R}^{n}\).
Atlas
An atlas \(C^{r}\) on a topological space \(M\) is a collection \(\left\{U_{\alpha},h_{\alpha}\right\}\) of charts. \(U_{\alpha}\) is an open covering admitted on \(M\) and \(h_{\alpha}\) is a homeomorphism on \(U_{\alpha}\) to the Eucledian space \(\mathbb{R}^{n}\). The \(C^{r}\) transition maps \(h_{\beta}h_{\alpha}^{-1}\) are \(C^{r}\) maps on \(h_{\alpha}(U_{\alpha}\cap U_{\beta})\).
Tangent Bundle
To continue.
Informal Manifold Definition
Short version: a manifold is a topological space that locally resembles Eucliden space.
Medium version: an \(n\)-dimensional manifold, or \(n\)-manifold, is a topological space where each point has a neighboorhood that is homeomorphic to an open subset on \(n\)-dimensional Euclidean space.
