Related Articles
Quantum Convolutional Neural Network
A quantum convolutional neural network combines two key techniques: multi-scale entanglement renormalization ansatz MERA, which is a variational ansatz for many-body wavefunctions, and nested quantum error correction QEC, which detects and corrects local quantum errors without collapsing the wavefunction. We will explore these two components, MERA and QEC, in detail. Next, we will look...
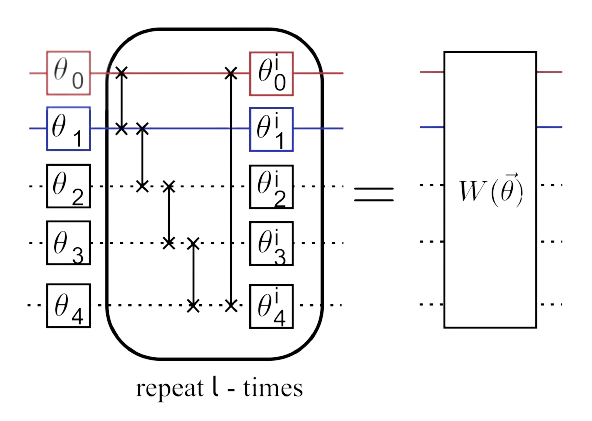
Quantum Support Vector Machine
Using quantum computing, the authors exploit quantum mechanics for the algorithmic complexity optimization of a Support Vector Machine with high-dimensional feature space. Where the high-dimensional classical data is mapped non-linearly to Hilbert Space and a hyperplane in quantum space is used to separate and label the data. By using the...
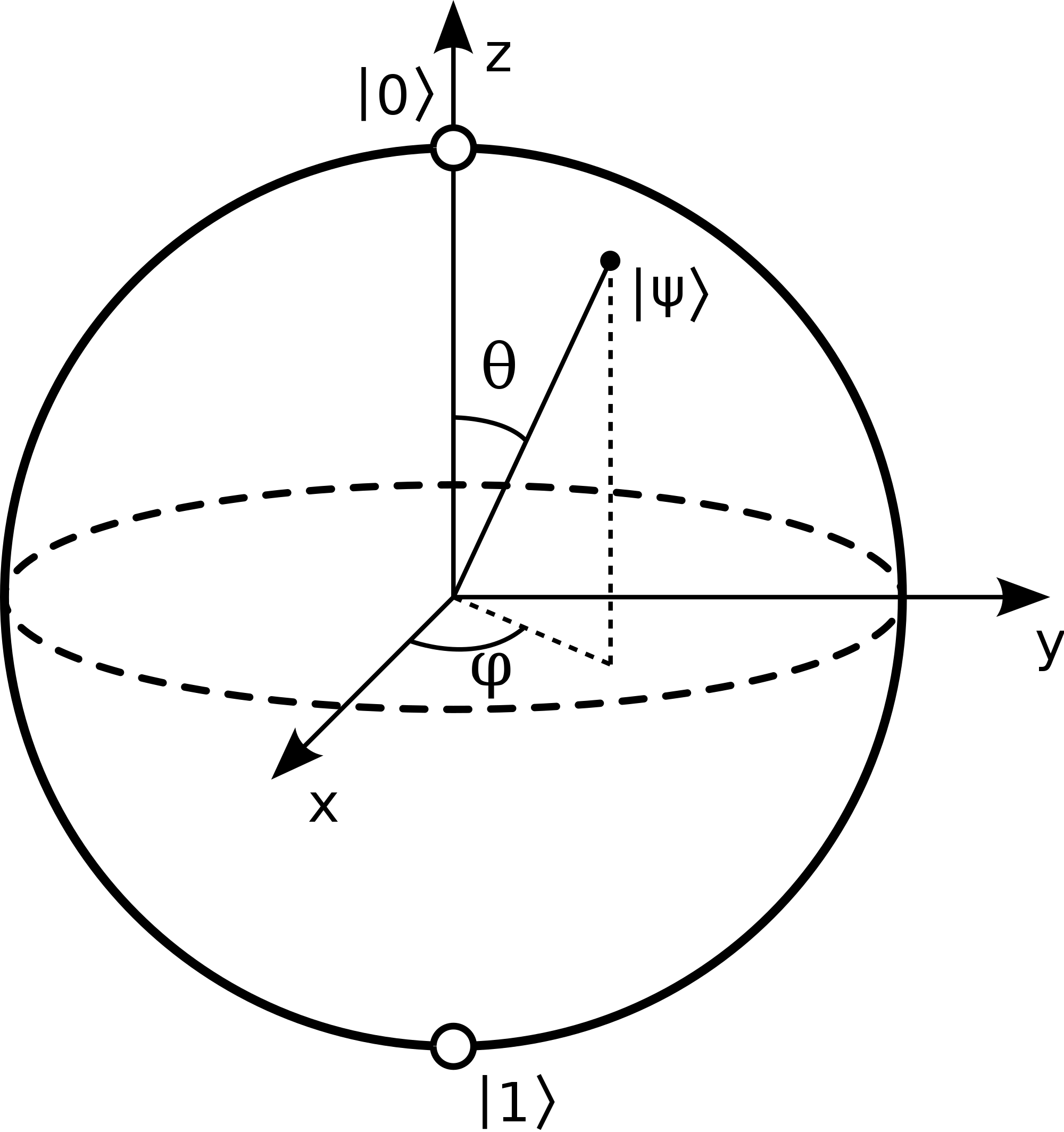
Quantum Computing Theory
Quantum Computing Theory is a field of computer science that uses the principles of quantum mechanics, mathematics, and computer science. By borrowing concepts from each field scientists can rigorously define both a broad and narrow theoretical model of a quantum computer and later apply it to the real world. These...