Topological Neuroscience
Graph theory is one main theoretical framework used to model, estimate, and simulate brain networks in complex network science. A graph is a composition of interconnected elements of vertices and edges, where vertices can represent neural structures and edges represent the functional connectivity between pairs of vertices. To reconstruct the brain network imaging modalities used are mainly the resting-state functional MRI rsfMRI. This imaging indirectly measures brain activity while a subject is at rest.
Graph Theory Preliminaries
Degree
The vertex degree quantifies the total numbers of vertex connections that exist in an uniderected binary network. The vertex degree for an undirected weighted network which represents the sum of all edges of the vertex and is equivalent to its degree centraility. We can look at the vertex degree anaglously to the vertex strength and is useful to give an idea of how densely individual vertices are connected. It is computed as:
\(C_{D}=s_{i}=\sum_{j\neq i}^{}w_{ij}\)
where \(w_{ij}\) is the respective weight of the edge that links vertex \(i\) and vertex \(j\).
Clustering Coefficent
\(Cl=\frac{2}{s_{i}(s_{i}-1)}\sum_{j,h}^{}(\hat{w}_{ij}\hat{w}_{jh}\hat{w}_{hi})^{\frac{1}{3}}\)
where \(s_{i}\) is the degree of vertex \(i\) and the edge wegihts are normalised by the maximum weight in the network. We can represent this normilization as: \(\hat{w}_{ij}=\frac{w_{ij}}{max(w)}\)
Centrailities
In order to measure a vertex's importance in a netwrok and consider its neightbour's influence we ascertain its eigenvector centrality which is degree-based. This is so we can consider both the vertices quantity and quality its connections. We can compute the eigenvector centraility by computing the spectra of the adjacency matrix \(Ax=\lambda x\). Where \(A\) represent the adjacency matrix and \(x\) is the eigenvector with a value of \(\lambda\) of \(A\). We can then define the eigenvector conetrality of some vertex \(i\) as:
\(C_{E}(i)=\frac{1}{\lambda_{1}}\sum_{j=1}^{N}A_{ij}x_{j}\)
Hypergraphs
Generally, hypergraphs is a graph where edges can join any number of vertices. An undirected hypergraph \(H\) can be defined as a pair \(H=(V,HE)\). Such that \(V\) represents the set of vertices and \(HE\) represents the set of hyperedges.
More Graph Theory Fun
This concludes most of the information neccesary for this page. However, if you are having fun with graph theory, feel free to read more on my Graph Theory page.
Multivariate Information Preliminary
Shannon Entropy
You can read about Shannon entropy in my Entropy and Average Code Length section. However, the important part to know is how to calculate the amount of uncertainty or suprise present in the probability distribution of a single random variable \(X\) or the Shannon entropy of \(X\). The Shannon Entropy, or just entropy, on \(X\) is denoted as \(H(X)\), given with a probabilty distribution of \(p(x)\), is defined as:
\(H(X)=-k\sum_{i=1}^{n}p_{i}\log_{2}(p_{i})\)
\(=\sum_{i=1}^{n}p_{i}\log_{2}\frac{1}{p_{i}}\)
where \(n\) represents the cartesian length of \(\left[N_{x}\right]=\left\{1,...N_{x}\right\}\) which is the codomain or alphabet of \(X\).
High-Order Functional Hubs in the Human Brain
Section Reference: Emergence of High-Order Functional Hubs in the Human Brain by: Fernando A.N. Santos, Prejaas K.B. Tewarie, Pierre Baudot, et al. \(^{[1]}\)
High-Order Neural Networks
Currently, neuroscience research predominantly focuses on a microscopic examination of neuronal architecture rooted in pairwise interactions. Consequently, mesoscopic and macroscopic studies inherit this dyadic perspective, which potentially provides an incomplete understanding of complex systems. Important observations like the regulatory role of astrocytes in both structural and synaptic plasticity. The authors cite that astrocytes regulate hetero-synaptic interactions as well as the heterogeneity of synaptic strength. These crucial regulatory astrocytes enable higher-order interactions, thus, forcing a shift in perspective of current neural interaction theories to incorporate higher-order structures.
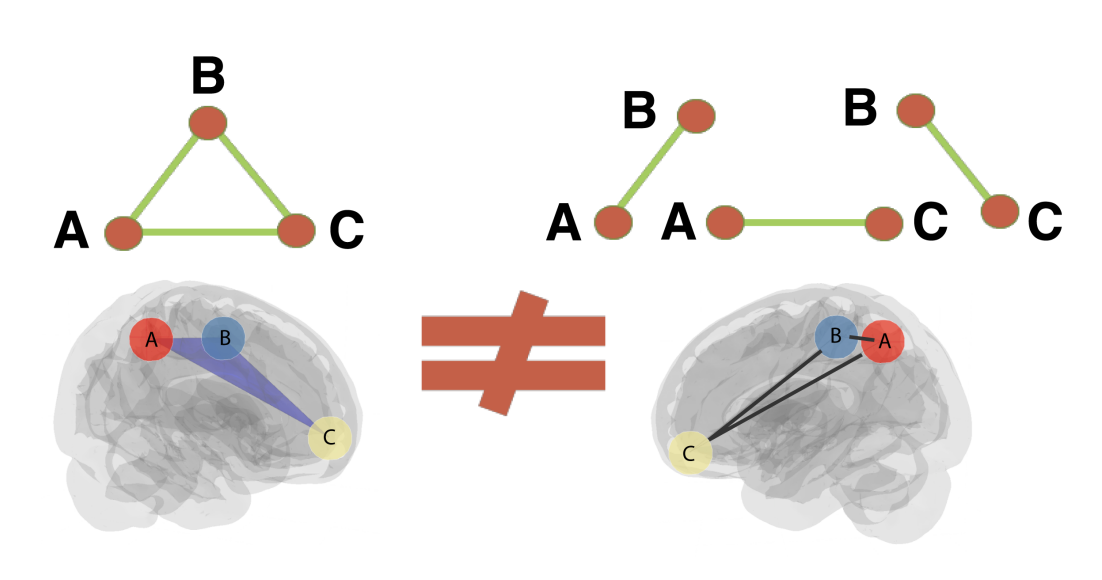
Image Source: See Reference [1]
Let's more cloesley examining why higher-order structures in brain networks is important for gaining a more informed neuroscientific understanding. The figure above illustrates the neccesity for the incorporation of such higher-order strcutures. This is because the illustration shows how interactions in higher-order complex systems, especially those in functional brain netwroks, are misrepresented as the approximations of the sum of pairwise interactions. However, the authors suggest, with a sutiable high-order connectivity rule, we can define higher-order hubs in a network, that will circumvent the combinitorial complexity assoicated with enumerating only the important high-order edges in known priority hyperedge networks.
Hypergraph Adjacency Matrix Algorithm
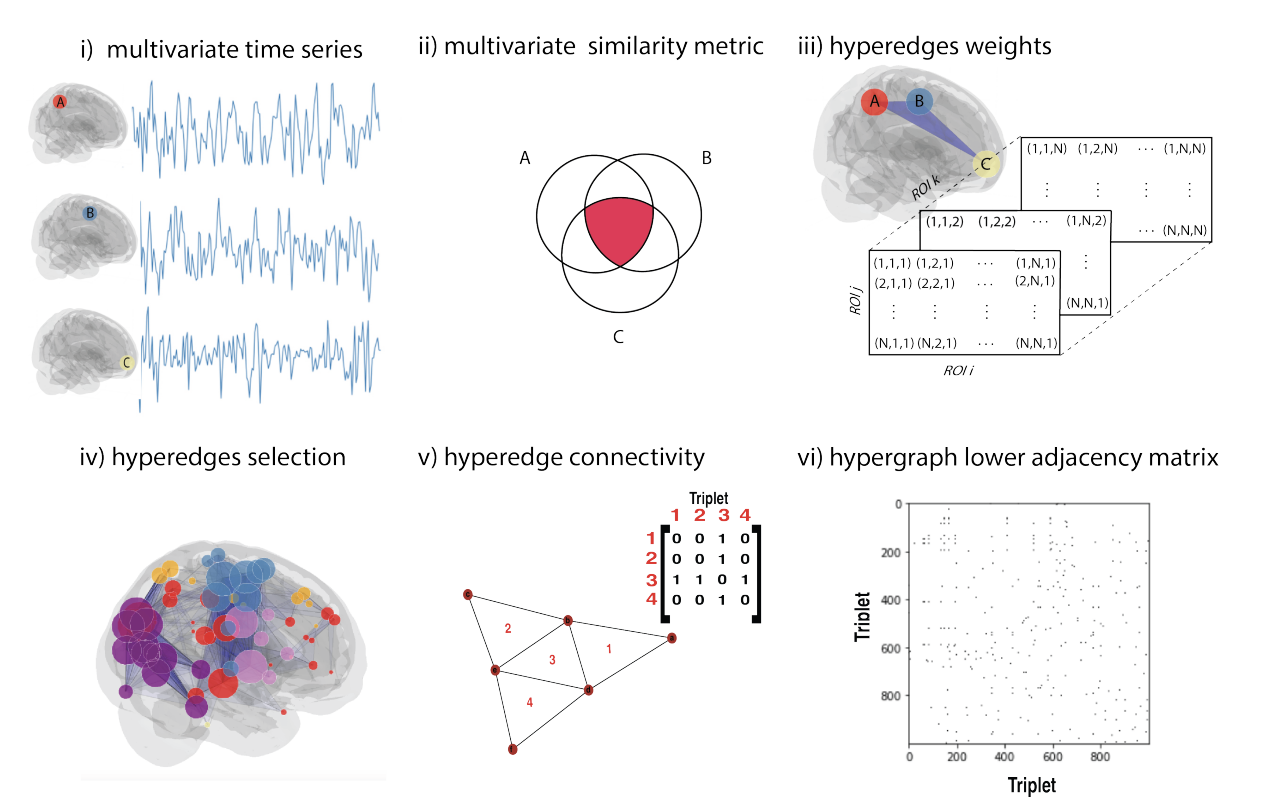
Image Source: See Reference [1]
The authors'\(^{[1]}\) algorithm for representing statistical structures of time series as hypergraphs is given in the five steps below and depicted in the figure above.
-
Let the input be an \(N\) time series. First, we must build the biological neural network hypergraph. Assign one node per time series. For all corresponding time series in the rsfMRI, each node represents a different brain region.
-
Next, choose an order \(k\in \left\{3,...,N\right\}\). Then, between all possible different groups of \(k\) nodes with a high-order interdependency metric, calculate the \(\binom{N}{k}\) \(k\)-order associated terms. The reason hypergraphs are chosen to represent pairwise connectivity, is because different multivariate similarities can be measured and considered. The authors focus on two infomraiton-theortic measures: Interaction Information and Total Correlation.
Interactive information quantifies a single tuple for statisical dependencies. Total Correlation quantifies the sum of all statisitcal dependencies over all tuple subsets.
-
For hyperedge selection, the number of \(k\)-order iteractions in \(N\) nodes grows as \(N^{k}\). Hypergprah, where significat network edges is choosen because of there representation of high-order connectivity.
-
The procedure used is to encode data relating to the encoding \(k\)-uniform hypergraph is termed a "hyper-adjacency matrix." A benefit of the hyper-adjacency matrix encoding is the representation of a low adjacency matrix representation for simplicial complexes in uniform hypergraphs. This encoding type can also be adapted to develop vector centralities in hypergraphs as well. Which is a good use case in topological neuroscience. Formally, two hyperedges of \(k\) dimensions are connected if they share a \(k-1\)-hyperedge.
-
The authors mentioned the final step in their algorithm, after multivariate signal processing and specification of the hyper-adjacency matrix, the topological features from network science can be applied. Here, given Eigenvector centrality, an extension of this is used to investigate high-order hubs in the human brain. Where, given hubs as triplets with higher eigenvector centrality, representing hyper-adjacency matrices the calculation of modularity and betweenness centrality in different neurological contexts.
To continue.
Total Correlation and the Brain's Visual System
To continue.
Glossary
Topolgical Space
You can read about topological space on my website here.
Resting State Functional Magnetic Resonance Imaging
Resting-state fMRI examines the brain's functional architecture by assessing spontaneous low-frequency fluctuations in the BOLD signal.