Compatification and Massless Scattering in Anti-de Sitter Space
In theoretical physics, Minkowski Space is a particular type of \(4\)-dimensional Lorentzian space, with a Minkowski metric. Where the Minkowski metric is a metric tensor denoted as \(d\tau^2\) with the form \(-\left(d^0\right)^2+\left(d x^1\right)^2\) \(+\;\left(d x^2\right)^2+\left(d x^3\right)^2\). Minkowski space forms the basis of the study of spacetime within special relativity and is the primary space we will use throughout.
Conformal Compactification of Asymptotically Flat Spacetimes
We first define a flat metric on Minkowski space, resembling the standard Minkowski metric, given in the spherical coordinates as:
\(d s^2=-d t^2+d r^2+2 r^2 \gamma_{z \bar{z}} d z d \bar{z}\)
Here, \(\gamma_{z \bar{z}}=\frac{2}{(1+z \bar{z})^2}\) is defined with polar coordinates \(z=e^{i \phi} \tan \frac{\theta}{2}\) and the spherical coordinates are projective coordinates for the \(S^{2}\) factor named the celestrial sphere \(CS^{2}\).
Next, let \(u, v \in(-\infty, \infty)\), where the finite range \(U,V \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) covers a given manifold. Next, we define new coordinates \((T,R)\), using the double null coordinates \((U,V)\) such that \(T=U+V\) and \(R=V-U\). The Minkowski metric \(ds^{2}\) relative to the coordinates \((T,R)\) is a conformal factor times the Lorentz metric on \(S^{3}\times\mathbb{R}\) and can be written as:
\(\begin{aligned} ds^{2} = & \left(\frac{L^2}{4 \cos ^2\left(\frac{R-T}{2}\right) \cos ^2\left(\frac{R+T}{2}\right)}\right) \\ & -d T^2+d R^2+2 \sin ^2 R \gamma_{z \bar{z}} d z d \bar{z} \\ = & \;\Omega^{-2} d \widetilde{s}^2 \end{aligned}\)
Here, our conformal factor is denoted as \(\Omega^{-2}\) and, as we can see from above, is defined as:
\(\Omega^{-2}=\frac{L^2}{4 \cos ^2\left(\frac{R-T}{2}\right) \cos ^2\left(\frac{R+T}{2}\right)}\)
An important property of this conformal factor is that it is positive, thus, preserving the casual structure for the rescaled metric \(d \widetilde{s}^2\). This is important, because preserving the casual structures in this compactification allows for curves that begin as timelike, null, or spacelike, to maintain as such with respect to the rescaled metric.
Next, we will attach a boundary to this compactification so that we can better understand the behavior of inifinity as it relates to Minkowski space and asymptotically flat spacetimes. These boundaries are given by the author, and are as folllows:
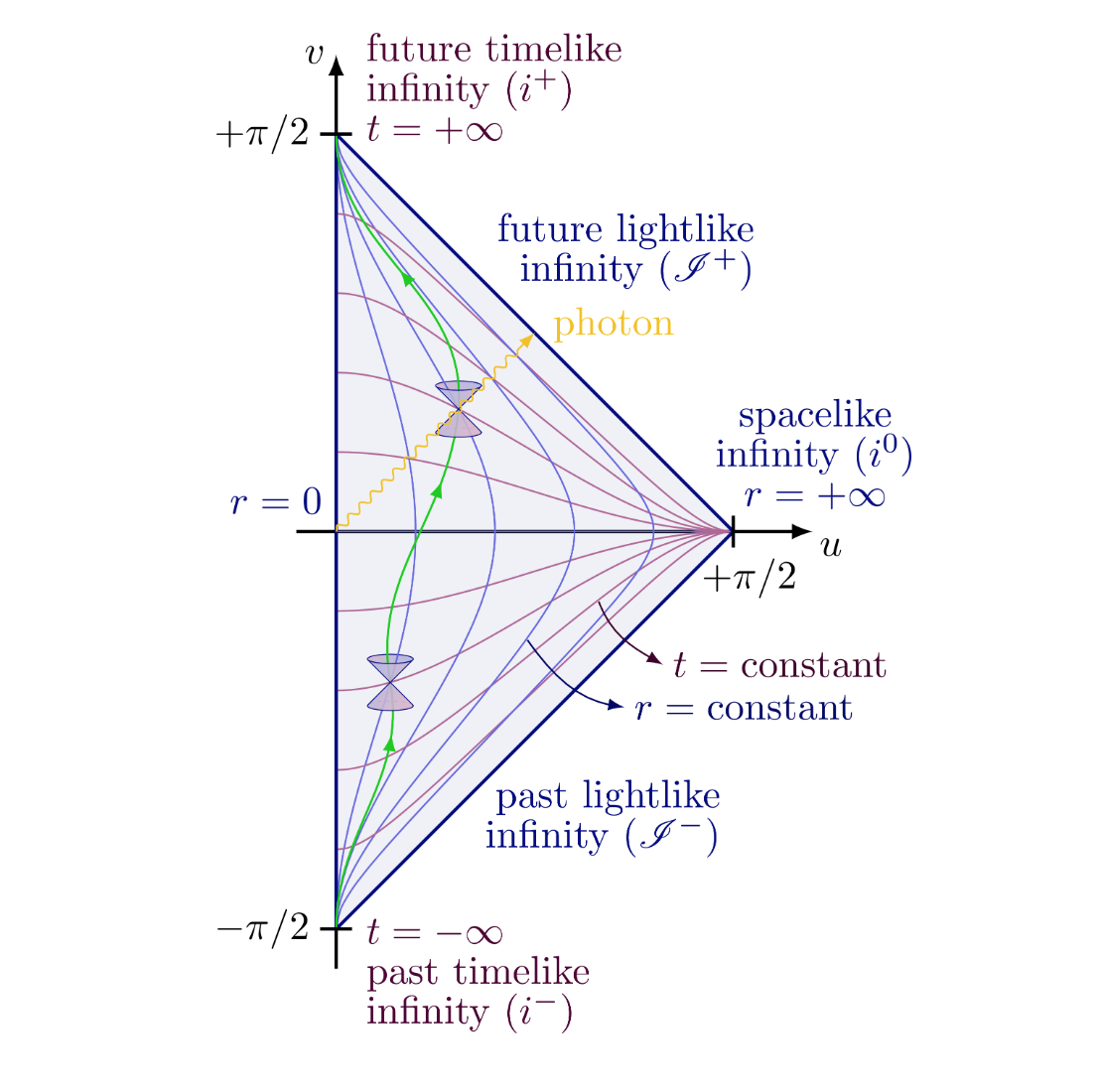
Image Source: https://tikz.net/relativity_penrose_diagram/
To continue.
Penrose Diagram of the Einstein Static Universe
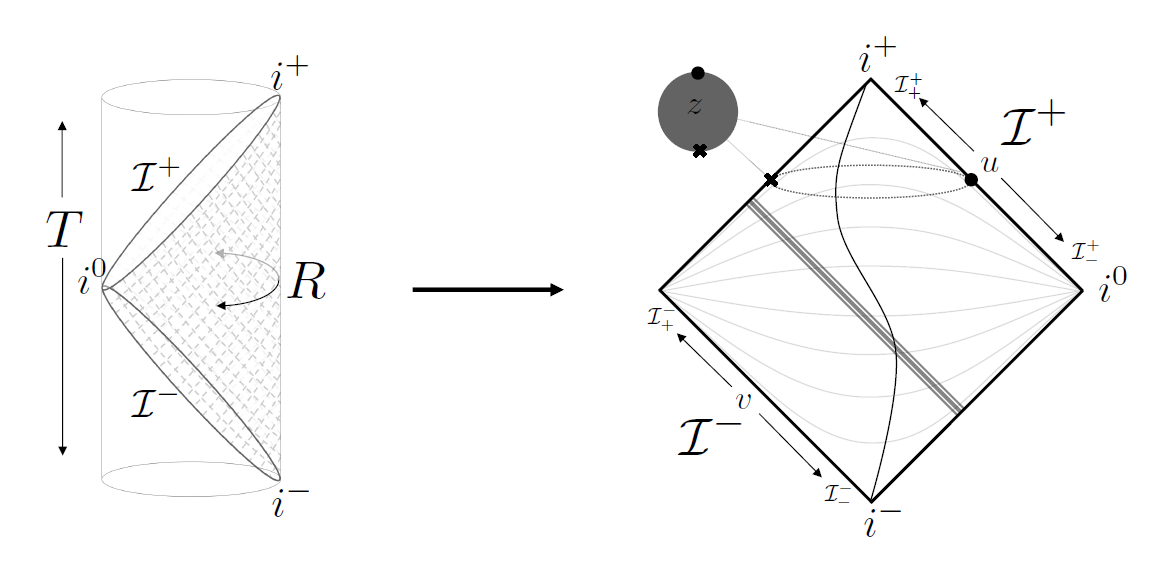
Image Source: [2]
Above is a Penrose diagram for Minkowski space that is represented as a patch of the Einstein static universe unwrapped, where the antipodal points are \(i^{-},i^{+}\). Massless trajectories travel at \(45^{\circ}\) to enter and exit at \(\mathcal{I}^{ \pm}\) while the geodesics for massive particles enter at \(i^{-}\) and exit at \(i^{+}\). Theoretically, many penrose-patches mathematically establish the space for white holes, parallel universes, antiverses, and Einstein-Rose bridges, however, I digress. I will probably learn and then write about this in the future though!
An example of a massless particles traveling at \(45^{\circ}\) through the Penrose diagram for Minkowski space are photons and lightcones, where a lightcone is a subdivision of Minkowski \(4\)-dimensional spacetime with respect to an event that has four disjoint sets. This all tells us that the Penrose diagram is conformal.
Geometry of Conformal Inversions
Four-dimensional Lorentzian space \(\mathbb{R}^{4}\) is know as Minkowski space and is denoted as \(\mathbb{M}=\mathbb{R}^{1,3}\), with the metric signature \((1,3)\) and the Cartesian coordinates \(X^\mu, \mu=0,1,2,3\). For this Lorentzian Space to be Minkowski Space, it must possess a type of metric tensor taken to be \(\eta_{\mu \nu}=\operatorname{diag}(-1,1,1,1)\), aptly named the Minkowski metric or Minkowski tensor. The light cone of the origin to null infinity is mapped using the conformal inversion map \(\mathbb{M}\). The reason being is the authors mention embeded space formalism is eaiser to study conformal transormations with conformal compactification of \(\mathbb{M}\).
Poincaré Patch on the Einstein Cylinder
Minkowski Spacetime and Lightcone
Minkowski spacetime is \(4\)-dimensional Eucledian space, with each point representing an event in space time. Such that, the fourth coordinate is an imaginary fourth spacetime coordinate. A subdivision of Minkowski spacetime with respect to an event that has four disjoint sets is called a light cone, portrayed below.
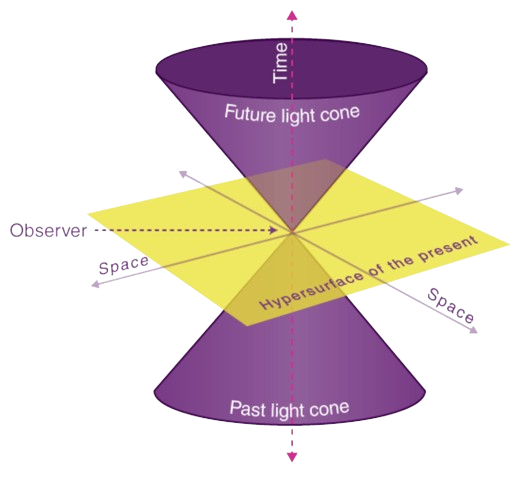
Image Source: https://byjus.com/physics/minkowski-space/
In this subdivision of Minkowski spacetime, there exists the absolute future, the absolute past, and elsewhere.
For a \(4\)-vector \(\mathbf{x}=(x_{0},x_{1},x_{2},x_{3})\) in Minkowski spacetime, variable \(x_{0}\) is time, while variables \(x_{1},x_{2},x_{3}\) are space variables. Furthermore, the time variable \(x_{0}\) is sometimes denoted \(t\), and when used in general relativity it can be denoted as \(c\) or \(i\;c\;t\). Where \(c\) represents the speed of light and \(i=\sqrt{-1}\) is an imaginary unit.
Celestrial Quadric
Let \(Z^{I}\) with index \(I=-1,0,...,4\) be coordinates on embedding space \(\mathbb{R}^{2,4}\) where the light cone of origin \(\mathbb{R}^{2,4}\) is cut out by:
\(\left(Z^{-1}\right)^2+\left(Z^0\right)^2\)\(=\left(Z^1\right)^2+\left(Z^2\right)^2+\left(Z^3\right)^2+\left(Z^4\right)^2\)
such that the origin \(Z^{I}=0\) is removed. The remaining light cone is positively rescaled with quotient \(Z^I \sim t Z^I, t \in \mathbb{R}_{+}\), arriving at Penrose's conformal compactification of \(\mathbb{M}\).
Given now that the light point does not contain an origin, it no longer contains points at \(Z^{-1}=Z^{0}=0\), meaning for the quoitent we can chose \(Z^{I}\) to satisfy:
\(\left(Z^{-1}\right)^2+\left(Z^0\right)^2\)\(=\left(Z^1\right)^2+\left(Z^2\right)^2+\left(Z^3\right)^2+\left(Z^4\right)^2\)\(=1\)
To do so, the authors mention performing the positive rescaling \(Z^{I}\rightarrow Z^{I}/\sqrt{(Z^{-1})^{2}+(Z^{0})^{2}}\), where the resulting space is topoglogically \(S^{1}\times S^{3}\).
This resulting topological space is a celestial quadric, such that the complement of the hyperplane in the space \(Z^{-1}+Z^{4}=0\) consists of two Poincaré Patches that are each a copy of \(\mathbb{M}\). The embeddings for the positive rescalings are defined as:
\(X^\mu \mapsto Z^I= \pm\left(\frac{1+|X|^2}{2}, X^\mu, \frac{1-|X|^2}{2}\right)\)
where \(|X|^2=\eta_{\mu \nu} X^\mu X^\nu\) is the Lorentzian norm.
To continue.
Glossary
AdS/CFT Correspondence
Anti-de Sitter/conformal theory correspondence AdS/CFT in theoretical physics is a conjecture that describes the relationship between two kinds of physical theories. AdS used in quantum gravtiy and is formulated in terms of string theory of M-theory, while, CFT are quantum field theories that include theories such as Yang-Mills theories describing elementatry particles.
Brane
Brane, in string theory and related supergravity theories, is a physical object thats use is to generalize the notion of a zero-dimensional point particle, a one-dimensional string, or a two-dimensional membrane to higher-dimensional objects.
Lorentzian Space
Lorentzian \(n\)-space is the inner product space of \(\mathbb{R}^{n}\) vector space with \(n\)-dimensional Lorentzian inner product. Where the vector space is a set that is closed under finite vector addition and scalar multiplication and inner product is defined as a vector space with an inner product on it.
Minkowski Space
The Minkowski Space is a particular type of Lorentzian space, specifically \(4\)-dimensional Lorentzian space, with a Minkowski metric or Minkowski tensor. Where the Minkowski metric is a type of metric tensor denoted as \(d \tau^2\) with the form \(-\left(d x^0\right)^2+\left(d x^1\right)^2+\left(d x^2\right)^2+\left(d x^3\right)^2\). Minkowski space forms the basis of the study of spacetime within special relativity. Another relative feature of this space is that it unifies \(\mathbb{R}^{3}\) plus time (the "fourth dimension") in Einstein's theory of special relativity.
Minkowski Metric
The Minkowski metric is defined as:
\(g_{\mu \nu} \approx \eta_{\mu \nu}=\left[\begin{array}{cccc}-1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\right]\)
Such that it is a metric of generally curved spacetime. One application of the Minkowski metric is modeling the cosmological constant term in Einstein's field equation with stress-energy from a vaccum or not.
Metric Signature
In theoretical physics, the metric signature counts the number of time-like or space-like characters are in the spacetime. For example, in the case Minkowski metric signature is \((1,3,0)^{+}\) or \((+,-,-,-)\) if the time direction is defined in the time direction. If the eigenvalue is defined in three spatial directions \(x,y,z\), then the metric signature is \((1,3,0)^{-}\) or \((-,+,+,+)\).