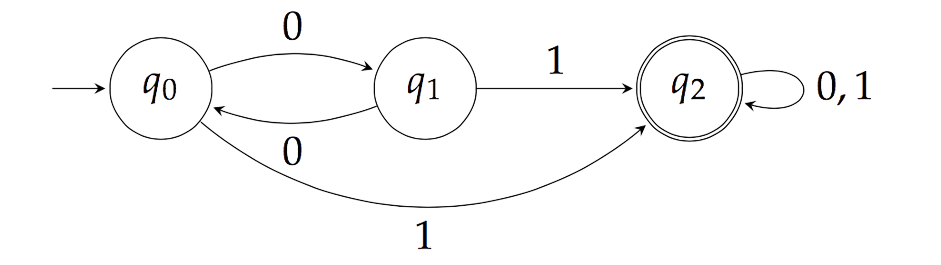
Deterministic Finite Automaton DFA

A deterministic finite automaton DFA is a 5-tuple:

\((Q, \Sigma, \delta, q_{0}, F)\)

where:

• \(Q\) is a finite set of states
• \(\Sigma\) is an alphabet
• \(\delta\) is a transition function described as \(\delta : Q \times \Sigma \rightarrow Q\)
• \(q_{0} \in Q\) is the initial state
• \(F \subseteq Q\) is a subset of states called accept states

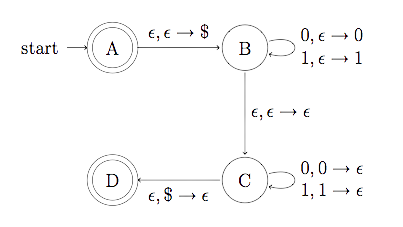
Pushdown Automaton PDA

A pushdown automata PFA is a 6-tuple:

\((Q, \Sigma, \Gamma, \delta, q_{0}, F)\)

where:

• \(Q\) is a finite set of states
• \(\Sigma\) is an alphabet
• \(\Gamma\) is the stack alphabet
• \(\delta\) is a transition function described as \(\delta : Q \times \Sigma \times \Gamma \rightarrow P(Q \times \Gamma_{\epsilon})\)
• \(q_{0} \in Q\) is the initial state
• \(F \subseteq Q\) is a subset of states called accept states

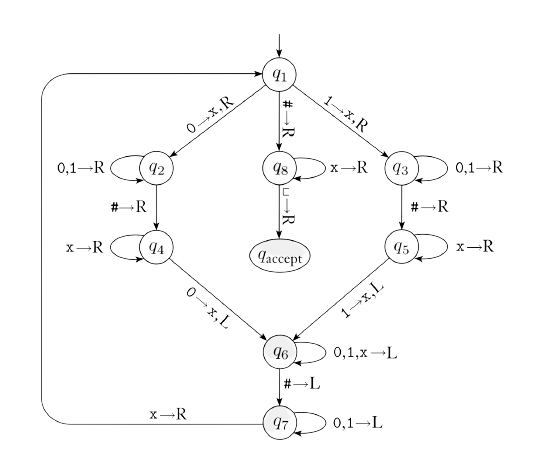
Basic Turing Machine

A Basic Turing Machine is a 7-tuple:

\((Q, \Sigma, \Gamma, \delta, q_{0}, q_{accept}, q_{reject})\)

where \(Q, \Sigma, \Gamma\) are all finite sets and:

• \(Q\) is a set of states
• \(\Sigma\) is an alphabet not containing the blank symbol \(\sqcup\)
• \(\Gamma\) is the tape alphabet, where \(\sqcup \in \Gamma\) and \(\Sigma \subseteq \Gamma\)
• \(\delta\) is a transition function described as \(\delta : Q \times \Sigma \rightarrow Q \times \Gamma \times \left\{L,\;R\right\}\)
• \(q_{0} \in Q\) is the initial state
• \(q_{accept} \in Q\) is the accept state
• \(q_{reject} \in Q\) is the reject state, where \(q_{reject} \neq q_{accept}\)

Linear-Bound Automaton (LBA)

To continue.